Opis problemu
W praktyce inżynierskiej przy wymiarowaniu najczęściej bazuje się na wynikach statyki liniowej. Efekty nieliniowe zostają uwzględnione poprzez współczynniki wyboczeniowe w przypadku konstrukcji stalowych [1, 3] oraz zwiększenie mimośrodu w przypadku konstrukcji żelbetowych [2, 4]. W obydwóch przypadkach konieczne staje się określenie siły krytycznej analizowanego elementu. Postępując zgodnie z proponowanymi przez normy procedurami [2-p.5.8.3.2, 3-Z1, 4-C, 5-E], przy określaniu siły krytycznej, należy określić możliwość wzajemnego przesuwu węzłów elementu – podział na układ o węzłach przesuwnych lub nieprzesuwnych. Przy schematach odbiegających od klasycznych, określenie „przesuwności” elementu/układu nie jest jednoznaczne. W normie [3] zawarto warunek (67) określający, że jeżeli dodanie stężeń zwiększa sztywność układu pięciokrotnie to może być traktowany jako nieprzesuwny. Pojawiają się dwa istotne pytania. Co się dzieje w sytuacjach pośrednich (zbyt mała sztywność stężeń) oraz czy warunek (67) może zostać uogólniony dla innych typów konstrukcji (np. żelbetowych)? Aby odpowiedzieć na powyższe pytania, analizie poddano wpływ wzrastającej sztywności poziomego stężenia (poziom rygla) ramy portalowej na wartość siły krytycznej oraz postać wyboczenia dla dwóch typów materiałów/przekrojów.
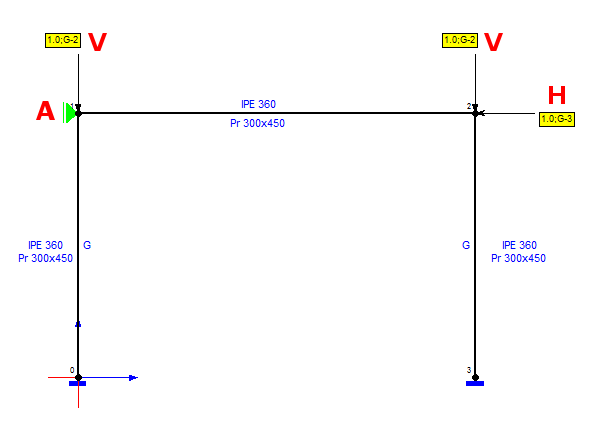
Rys.1. Model analizowanej ramy portalowej
Metody
Analizie poddano dwie ramy portalowe: stalową wykonaną z dwuteowników (S235) oraz, w celu uogólnienia wyników, betonową o prostokątnym przekroju słupów i rygla (C35/45, pominięto efekty zarysowania, reologiczne oraz wpływ zbrojenia). Modele obliczeniowe zdefiniowano w programie Soldis PROJEKTANT v8.5 (Rys.1) (więcej o definicji modeli tutaj, model załączono do niniejszego dokumentu). Stężenia uwzględniono w uogólniony sposób poprzez podporę (Rys.1.A) z możliwością przesuwu w pionie i zmienną podatnością w kierunku poziomym. Malejąca podatność odpowiada wzrastającej sztywności stężeń poziomych. Przyjęte podejście pozwala na analizowanie zmiany sztywności stężeń bez względu na sposób ich konstrukcji. Słupy obciążono pionową siłą jednostkową (Rys.1.V). W celu określenia sumarycznej sztywności stężeń i układu, w niezależnym schemacie obciążenia, wprowadzono jednostkową siłę poziomą (Rys.1.H).
Przygotowano serię 22 modeli obliczeniowych (11 dla każdej ramy) dla malejącej podatności podpory-stężenia. Wartość podatności zmieniała się od 1e-6m/kN do 1e-9m/kN. Dla każdego modelu wykonano obliczenia statyczne i odczytano przemieszczenie poziome rygla od siły H oraz określono, na jej podstawie, tangens kąta obrotu cięciwy słupów, parametr Ψ=tan(α) [patrz 3,(67) oraz Rys.2] (otrzymane przemieszczenie podzielono przez wysokość ramy). Następnie wykonano analizę stateczności (panel główny > Analiza > Stateczność) uzyskując mnożnik siły krytycznej równy w analizowanym przykładzie, co do wartości, sile krytycznej wyrażonej w kN (siła normalna w słupach od przyjętego obciążenia wynosi 1kN). W celu łatwiejszej interpretacji wyników, określono dodatkowo współczynnik długości wyboczeniowej słupów zgodnie z procedurą opisaną tutaj.
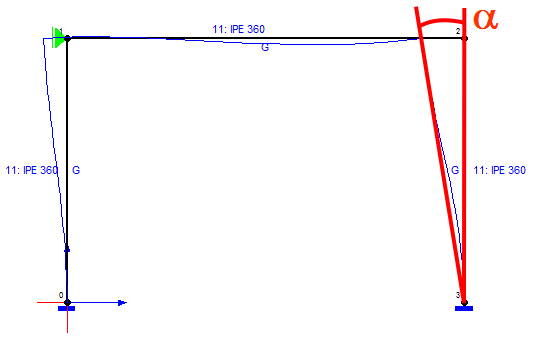
Rys.2. Sposób określania cięciwy obrotu słupa pod działaniem jednostkowego obciążenia poziomego
Wyniki
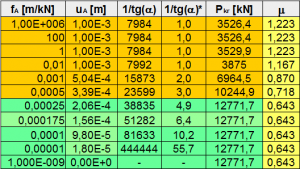
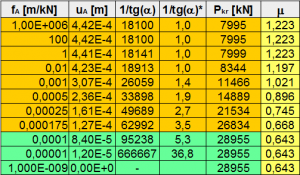
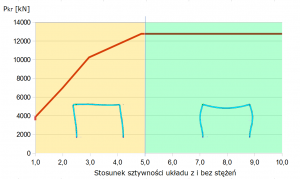
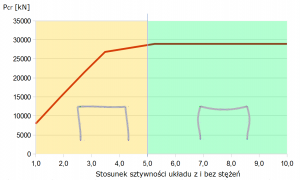
Otrzymane wyniki przedstawiono na rysunkach 3, 4 oraz 5. Wartość fA i uA oznacza podatność poziomą podpory-stężenia oraz poziome przemieszczenie węzła górnego od siły H. Interpretacje kąta α przedstawiono na Rys.2. Współczynnik długości wyboczeniowej słupa oznaczono μ. Wartość 1/tg(α)* jest stosunkiem sztywności układu stężonego do sztywności układu bez stężeń (największa podatność).
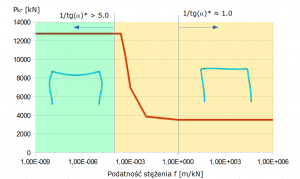
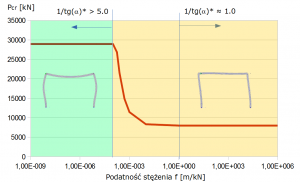
Kolorem zielonym i pomarańczowym rozróżniono wiersze oraz obszary wykresu, gdzie dominowała utrata stateczności poprzez obrót węzłów lub przesuw rygla górnego – układ odpowiednio o węzłach nieprzesuwnych lub przesuwnych.
| Rama stalowa | Rama żelbetowa |
|---|---|
 |
 |
| Rys.3. Wyniki szczegółowe analizy statycznej oraz stateczności. | |
 |
 |
| Rys.4. Zależność siły krytycznej od podatności stężeń. | |
 |
 |
| Rys.5. Zależność siły krytycznej od wzrostu sztywności w wyniku zastosowania stężeń. | |
Dyskusja
Bez względu na zastosowany materiał, wraz ze wzrastającą sztywnością podpory-stężenia maleje przemieszczenie uA (poziome rygla od siły jednostkowej H) co z kolei powoduje wzrost sztywności układu mierzony jako 1/tg(α) oraz zwiększenie wartości siły krytycznej (spadek wsp. długości wyboczeniowej). Analizując Rys.4 można wyodrębnić strefę przejściową między postacią/siłą krytyczną dla układu całkowicie stężonego oraz bez stężeń. Mimo wzrastającej sztywności stężeń, w obszarze przejściowym, postać „przechyłowa” utraty stateczności jest dominująca. Po przekroczeniu pewnego progu sztywności, postać utraty stateczności ulega gwałtownej zmianie i dominują obroty w węzłach (układ nieprzesuwny). Zmiana postaci wyboczenia następuje dla stężeń zwiększających całkowitą sztywność ramy 4.8 oraz 5.3-krotnie odpowiednio dla ramy stalowej i żelbetowej (betonowej).
UWAGA! W niniejszych analizach przyjęto niekorzystny schemat obciążenia – jednakowe ściskanie słupów – elementy tracą stateczność jednocześnie i nie wpływają na sztywność poziomą na wysokości rygla. Przy nierównomiernym obciążeniu słupów należy spodziewać się obniżenia wspomnianego progu sztywności.
Podsumowanie
Analiza uzyskanych wyników potwierdza, że dla analizowanych ram, 5-krotne zwiększenie sztywności układu w wyniku zastosowania stężeń zapewnia postać wyboczenia oraz wartość siły krytycznej taką samą jak przy całkowitym zablokowaniu możliwości przesuwu węzłów (układ nieprzesuwny). Dla niewystarczająco sztywnego stężenia, siła krytyczna stopniowo maleje, aż do wartości wyznaczonej dla układu o węzłach przesuwnych. Aby uwzględnić wzrost siły krytycznej dla stężeń, które nie spełniają warunku (67) w [3], należy przeprowadzić analizę zgodnie z zaprezentowaną procedurą.
W przypadku wymiarowania konstrukcji żelbetowych według [2] lub [4] siła krytyczna powinna zostać wyznaczona z uwzględnieniem zastosowanego zbrojenia, zarysowania i efektów reologicznych (dla wszystkich elementów, ściskanego i z nim połączonych). W tym celu można zmodyfikować sztywność zgodnie z p.5.8 w [2] (sztywność nominalna) lub, korzystając z normy [4], według wzoru (38) (przybliżona sztywność giętna określona jest w nawiasie kwadratowym). Przeprowadzone analizy wykazały słuszność warunku (67) w [3] dla dwóch różnych sztywności elementów ramy (różne przekroje i materiały). Dlatego też, jeżeli uwzględnienie rzeczywistej sztywności elementu żelbetowego będzie dokonywane poprzez korektę sztywności giętnej na całej jego długości, a nie tylko w obszarach silnie zginanych, powyżej sformułowane wnioski nie powinny ulec zmianie.
UWAGA! Wyniki uzyskano dla konkretnej konfiguracji geometrii, obciążenia i przekrojów elementów prętowych ramy. Uogólnianie powyżej sformułowanych wniosków na inne typy konstrukcji jest obarczone ryzykiem. W przypadku wątpliwości należy przeprowadzić powyższą procedurę dla analizowanego układu.
Bibliografia
- PN-EN 1993-1-1 „Projektowanie konstrukcji stalowych: Reguły ogólne i reguły dla budynków”
- PN-EN 1992-1-1 „Projektowanie konstrukcji z betonu: Reguły ogólne i reguły dla budynków”
- PN-90/B-03200 „Konstrukcje stalowe: Obliczenia statyczne i projektowanie”
- PN-B-03264 „Konstrukcje betonowe, żelbetowe, sprężone: Obliczenia statyczne i projektowanie”
- DD ENV 1993-1-1:1992 „Design of steel structures. General rules and rules for buildings”
Załączniki do pobrania
| Plik | Opis | Wielkość pliku | Pobrania |
|---|---|---|---|
Wpływ sztywności stężeń - rama żelbetowa
|
43 KB | 1159 | |
|
Wpływ sztywności stężeń - rama stalowa
|
44 KB | 940 |
