Opis problemu
Zastosowanie wyników statyki liniowej do wymiarowania wymusza uwzględnienia efektów nieliniowych w sposób pośredni. Normy [1, 2, 3, 4] określają wzrost sił przekrojowych/naprężeń w funkcji siły krytycznej elementu, która ściśle zależy od długości wyboczeniowej będącej iloczynem długości rozpatrywanego elementu oraz współczynnika długości wyboczeniowej. Określenie współczynnika dł. wyboczeniowej dla relatywnie prostych przypadków można przeprowadzić wg [2, p.5.8.3.2], [3, Z1], [4, C] oraz [5, E]. W pozostałych sytuacjach projektant zobowiązany jest określić długość wyboczeniową samodzielnie, na przykład na bazie analizy numerycznej (p.5.8.3.2(6) w [2]). W poniższym dokumencie przedstawiono ogólną procedurę określania siły krytycznej i wsp. długości wyboczeniowej na podstawie analizy stateczności początkowej (problem własny).
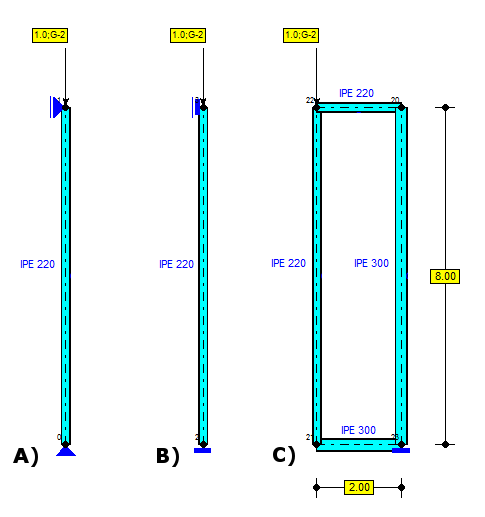
Rys.1. Modele analizowanych elementów ściskanych
Metody
Analizie poddano trzy konstrukcje wykonane z dwuteowników (stal S235) (Rys.1). Ponieważ dwie pierwsze reprezentują klasyczne przypadki, a wyniki są łatwe do określenia zgodnie z wzorem poniżej, posłużą one do weryfikacji przyjętej procedury.![]()
Dla każdego przypadku zdefiniowano model w programie Soldis PROJEKTANT v8.5 (więcej o definicji modeli tutaj, modele załączono do niniejszego dokumentu), gdzie przyjęto schemat obciążenia powodujący dominujące ściskanie w analizowanym pręcie (w praktycznym zastosowaniu należy przyjąć miarodajny schemat obciążenia przy którym występuje utrata stateczności). W pierwszym kroku procedury wykonano analizę statyczną w celu określenia siły normalnej w analizowanym elemencie. Następnie wykonano analizę stateczności (pasek główny > Analiza > Stateczność) odczytując wartość mnożnika siły krytycznej lambda. Ostateczną wartość siły krytycznej ustalono jako iloczyn siły normalnej w elemencie i mnożnika lambda. W celu określenia wsp. długości wyboczeniowej, uzyskaną wartość siły krytycznej, Pkr(μ), odniesiono do analitycznej wartości siły krytycznej dla schematu A (μ=1.0). Po drobnych transformacjach i przekształceniach otrzymujemy:
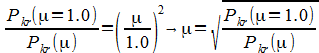
lub alternatywnie zgodnie z wzorem 5.17 w [2]:
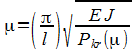
Wyniki
Siła krytyczna dla przypadku A wyznaczona zgodnie z analitycznym wzorem Eulera wynosi:
![]()
Uzyskane mnożniki sił krytycznych, siły normalne oraz obliczone siły krytyczne i współczynniki długości wyboczeniowej przedstawiono w Tab.1. Na Rys. 2 przedstawiono rozkład sił normalnych, a na Rys.3 postacie utraty stateczności.
Tab.1: Zestawienie wartości sił normalnych, krytycznych oraz wsp. dł. wyboczeniowej
| Model | Lambda | N [kN] (statyka) | Siła krytyczna [kN] |
Wsp. dł. wyboczeniowej [-] | |
|---|---|---|---|---|---|
| Otrzymany | Teoretyczny | ||||
| A | 898.5 | 1.0 | 898.5 | 0.999 | 1.0 |
| B | 3666.8 | 1.0 | 3666.8 | 0.495 | 0.5 |
| C | 2142.3 | 0.935 | 2003.0 | 0.669 | – |
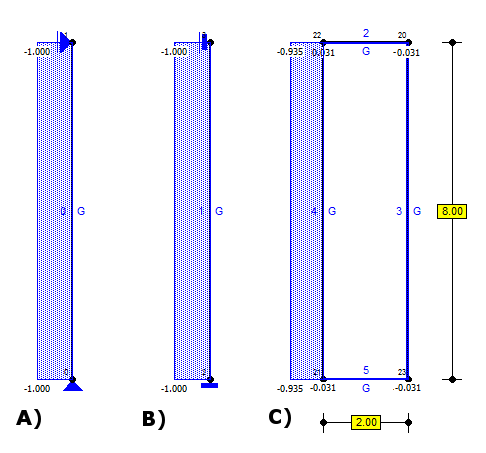 Rys.2. Wykres siły normalnej od przyjętego obciążenia
Rys.2. Wykres siły normalnej od przyjętego obciążenia
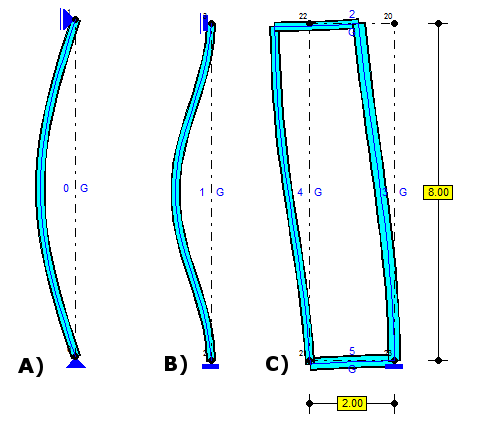 Rys.3. Postacie utraty stateczności
Rys.3. Postacie utraty stateczności
Podsumowanie
Współczynniki długości wyboczeniowej otrzymane w przypadkach A i B są zgodne z teoretycznymi wartościami (błąd <1%) co potwierdza prawidłowość zaprezentowanej procedury. Przypadek C jest ilustracją ogólniejszej sytuacji ze sztywnością obrotową oraz poziomą w węźle górnym i dolnym. Zaprezentowana procedura może zostać użyta dla elementu dowolnie podpartego. Dodatkową zaletą jest brak konieczności określania czy istnieje możliwość wzajemnego przesuwu węzłów elementu (układ o węzłach przesuwnych/nieprzesuwnych) – analizujemy rzeczywistą sztywność na obrót cięciwy elementu.
Przedstawiony przykład bazował na konstrukcji stalowej. W przypadku wymiarowania konstrukcji żelbetowych według [2] lub [4] siła krytyczna powinna zostać wyznaczona z uwzględnieniem zastosowanego zbrojenia, zarysowania i efektów reologicznych (dla wszystkich elementów, ściskanego i z nim połączonych). W tym celu należy zmodyfikować sztywność zgodnie z p.5.8 w [2] (sztywność nominalna) lub, korzystając z normy [4], według wzoru (38) (przybliżona sztywność giętna określona jest w nawiasie kwadratowym).
Bibliografia
- PN-EN 1993-1-1 „Projektowanie konstrukcji stalowych: Reguły ogólne i reguły dla budynków”
- PN-EN 1992-1-1 „Projektowanie konstrukcji z betonu: Reguły ogólne i reguły dla budynków”
- PN-90/B-03200 „Konstrukcje stalowe: Obliczenia statyczne i projektowanie”
- PN-B-03264 „Konstrukcje betonowe, żelbetowe, sprężone: Obliczenia statyczne i projektowanie”
- DD ENV 1993-1-1:1992 „Design of steel structures. General rules and rules for buildings”