Opis problemu
Podparcie punktowe reprezentujące słup w ustrojach płytowo-słupowych powoduje powstanie lokalnych zaburzeń. Momenty gwałtownie rosną w miarę zbliżania się do podpory. Dodatkowo wartość maksymalna zmierza do nieskończoności w miarę zagęszczania siatki. W konsekwencji próba ustalenia zbrojenia dla maksymalnego momentu nie jest zasadna. Zgodnie z zasadą de Saint-Venanta zaburzenia lokalne zanikają w miarę oddalania się od podpory (siły skupionej) i w pewnej odległości mogą być pominięte. Wciąż jednak aktualnym problemem jest ustalenie „bezpiecznej” odległości, gdzie wpływ zaburzeń może być zaniedbany. Powszechnie stosowanym rozwiązaniem jest odczyt wartości w licu słupa lub ściany. W niniejszym przykładzie wykonano studium wpływu gęstości siatki na wartości momentów w okolicy podpory punktowej dla różnej grubości płyty i rozpiętości przęseł oraz sprawdzono czy zaburzenia lokalne zanikają w na krawędzi słupa.
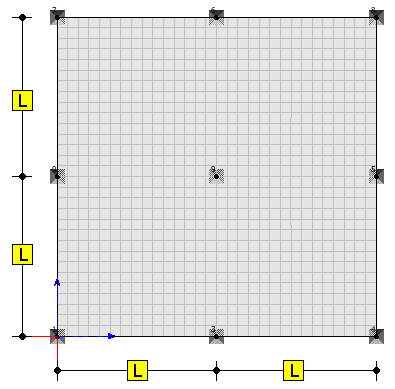Rys.1. Analizowany ustrój płytowo-słupowy
Metody
Analizie poddano podparcie punktowe reprezentujące słup środkowy w układzie płytowo-słupowym zgodnie z Rys.1. Rozpatrywano dwie rozpiętości przęseł L=6.0m oraz L=4.0m oraz grubości płyty t=0.1m oraz t=0.2m. Wszystkie podpory umożliwiają swobodny obrót. Przyjęto obciążenie ciężarem własnym oraz powierzchniowe, równomiernie rozłożone, o wartości 2.0kN/m2 Dla stopniowo zagęszczanej siatki porównano przebieg momentów Mx wzdłuż poziomej osi symetrii przechodzącej przez podporę środkową. Analizowane siatki elementów skończonych oznaczono S1, S2, S3 oraz S4 i zaprezentowano na Rys.2 oraz Rys.3. Przyjęto Beton C30/37 oraz wymiar słupa 0.4×0.4m. Obliczenia wykonano w programie Soldis PROJEKTANT 2017.
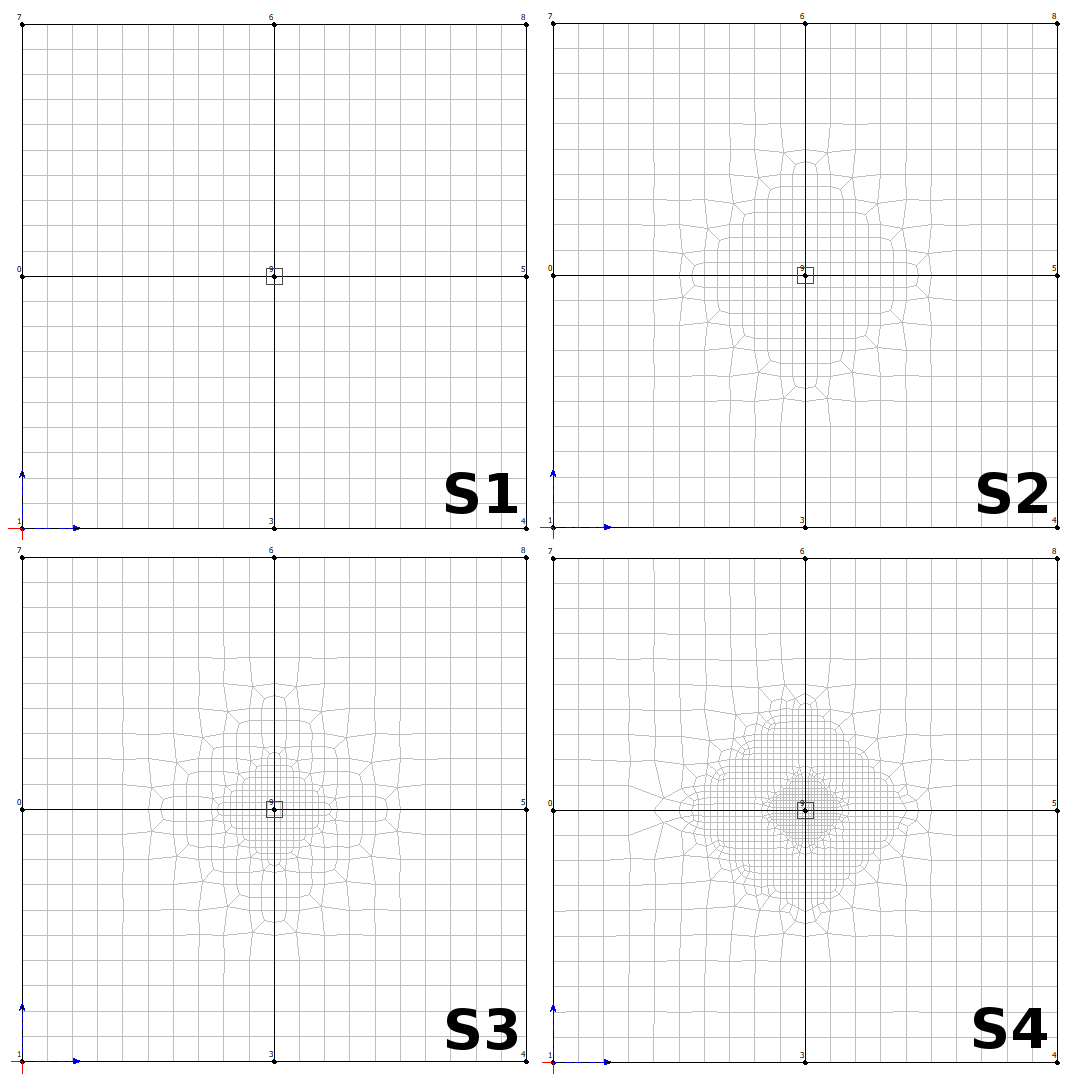
Rys.2. Analizowane siatki elementów skończonych (gabaryty słupa są tylko prezentacją graficzną i nie są obecne w modelu).
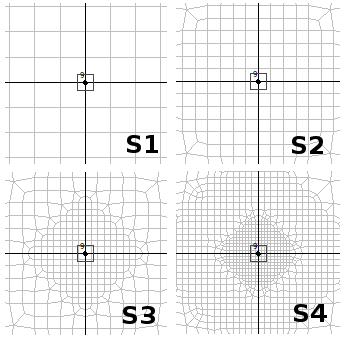Rys.3. Obszar słupa środkowego dla analizowanych siatek.
Wyniki
W Tab.1 zestawiono wartości Mx wzdłuż poziomej osi symetrii dla czterech siatek elementów skończonych. Rys.4 zawiera graficzną prezentację danych z Tab.1 z zaznaczeniem obszaru w obrysie słupa. Znacząca różnica w wynikach między siatką S1 i S2 wskazuje na zbyt duże elementy w siatce S1. Ze względu na powyższe, wyniki dla siatki S1 zostaną pominięte w dalszej analizie.
Tab.1: Zestawienie maksymalnej wartości momentu Mx nad podporą punktową dla różnych siatek elementów skończonych
| L=6m t=0.1m | ||||
|---|---|---|---|---|
| x | S1 | S2 | S3 | S4 |
| -1.6 | 1,808 | 1,539 | 1,985 | 1,673 |
| -1.4 | -1,114 | -1,346 | -1,26 | -1,195 |
| -1.2 | -5,844 | -4,857 | -4,755 | -4,739 |
| -1.0 | -12,725 | -9,246 | -9,065 | -9,295 |
| -0.8 | -20,269 | -14,065 | -14,072 | -13,619 |
| -0.6 | -26,718 | -21,973 | -20,932 | -20,776 |
| -0.4 | -30,767 | -36,463 | -29,822 | -30,274 |
| -0.2 | -32,928 | -47,338 | -53,485 | -46,456 |
| 0.0 | -34,569 | -52,474 | -69,485 | -86,261 |
| L=6m t=0.2m | ||||
|---|---|---|---|---|
| x | S1 | S2 | S3 | S4 |
| -1.6 | 4,495 | 2,89 | 3,347 | 3,313 |
| -1.4 | 0,225 | -1,405 | -1,423 | -1,319 |
| -1.2 | -6,563 | -6,631 | -7,293 | -7,222 |
| -1.0 | -16,903 | -13,203 | -13,647 | -14,04 |
| -0.8 | -28,804 | -20,377 | -21,452 | -20,516 |
| -0.6 | -38,031 | -32,552 | -31,602 | -31,648 |
| -0.4 | -45,739 | -55,791 | -45,778 | -46,514 |
| -0.2 | -50,044 | -73,093 | -81,664 | -71,672 |
| 0.0 | -53,119 | -80,825 | -107,057 | -133,152 |
| L=4m t=0.2m | ||||
|---|---|---|---|---|
| x | S1 | S2 | S3 | S4 |
| -1.6 | 6,997 | 6,716 | 6,613 | 6,765 |
| -1.4 | 5,312 | 5,08 | 4,951 | 5,159 |
| -1.2 | 3,351 | 3,02 | 2,673 | 3,124 |
| -1.0 | 1,169 | 0,429 | 0,179 | 0,546 |
| -0.8 | -2,946 | -2,869 | -3,396 | -2,858 |
| -0.6 | -10,196 | -7,341 | -6,743 | -7,298 |
| -0.4 | -17,424 | -14,343 | -13,749 | -13,719 |
| -0.2 | -21,255 | -29,235 | -25,694 | -24,828 |
| 0.0 | -23,55 | -35,667 | -47,163 | -58,089 |
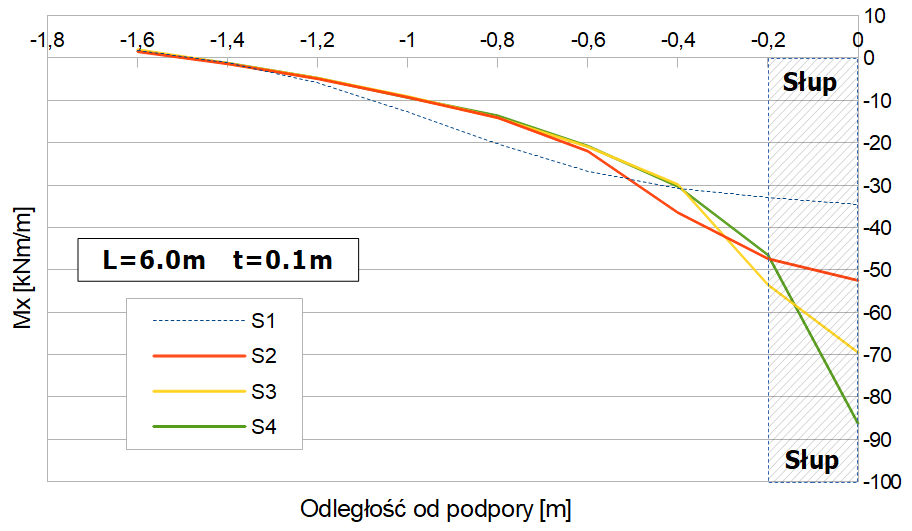
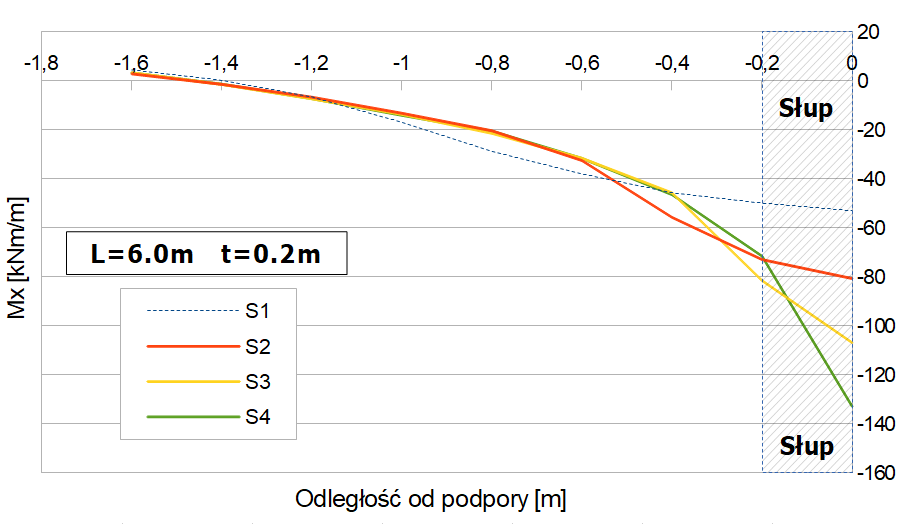
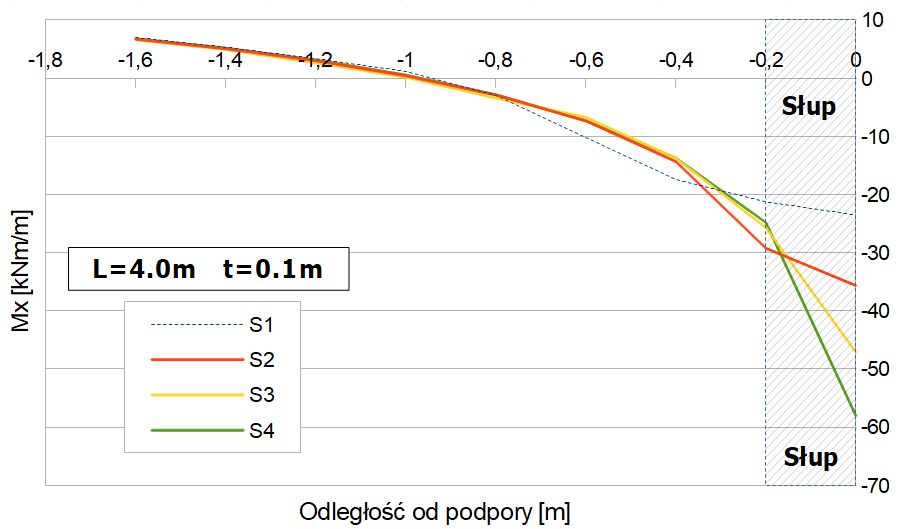Rys.2. Zmiana Mx w funkcji odległości od podpory dla różnych grubości płyty oraz rozmiarów przęsła.
Tab.2: Różnica wartości Mx w licu ściany w odniesieniu do wyników uzyskanych dla siatki S4 [w procentach]
| S2 | S3 | S4 | |
|---|---|---|---|
| L=6m t=0.1 | 1,90 | 15,13 | 0,0 |
| L=6m t=0.2 | 1,98 | 13,94 | 0,0 |
| L=4m t=0.2 | 1,98 | 13,94 | 0,0 |
Podsumowanie
Otrzymane wyniki potwierdzają dwa zjawiska: zagęszczanie siatki zwiększa moment nad podporą oraz zaburzenia od podpory punktowej maleją w miarę oddalania się od niej (Tab.1 i Rys.2).
W analizowanym przypadku odchylenie wartości Mx w licu słupa dla poszczególnych siatek, grubości oraz rozpiętości przęseł różni się maksymalnie o 15% (około 7kNm/m, Tab.2), a wyższa wartość dla siatki S3 względem siatki S4 dowodzi, że różnica jest naturalnym efektem topologii siatek (interpolacja wyników z punktów całkowania do punktów wzdłuż przekroju), a nie ich gęstości. Dla siatki S2 różnica nie prekracza 2%. Należy dodatkowo zwrócić uwagę, że zagęszczanie siatki powoduje zbieżność do wyniku teoretycznego z pewnymi oscylacjami i określanie „błędu” jako różnicy względem wyników dla siatki S4 może go zawyżać. Warto również zwrócić uwagę, że stosując podpory punktowe zwiększamy obliczeniową rozpiętość przęsła. W konsekwencji otrzymany moment jest zawyżony i może kompensować ewentualne niedoszacowanie momentu dla rzadszej siatki (z wyłączeniem S1).
Na podstawie uzyskanych wyników można stwierdzić, że dla analizowanej konstrukcji zaburzenia lokalne nad podporą tracą na praktycznym znaczeniu w okolicach lica słupa.
Wynik wskazują również na konieczność zagęszczenia siatki w okolicach podpory punktowej (patrz wyniki dla siatki S1) i w analizowanym przykładzie satysfakcjonujące wyniki uzyskano już przy siatce S2 – rozmiar elementu przy podporze równy 0.3m (1/20L).
Załączniki do pobrania
| Plik | Opis | Wielkość pliku | Pobrania |
|---|---|---|---|
model_osobliwosc
|
88 KB | 1015 |
