Opis problemu
Połączenie teleskopowe definiowane jest między dwoma węzłami i umożliwia ich wzajemne przemieszczenie wzdłuż wskazanego kierunku blokując jednocześnie względne obroty oraz przemieszenia w kierunku prostopadłym (Rys.1). Ilustracją może być połączenie dwóch rur poprzez nasunięcie na nie rury o większej średnicy (założenie idealnego poślizgu, Rys.2). Połączenie teleskopowe jest często stosowane w celu eliminacji sił normalnych w elemencie lub/i jego podłużnej sztywności. Niniejszy dokument ilustruje sposób definiowania połączenia teleskopowego w programie Soldis PROJEKTANT v8.5 (plik modelu dołączono do dokumentu).
Metody
Procedura modelowania połączenia została zaprezentowana na przykładzie 10 metrowej belki wolnopodpartej (IPE330) podzielonej na dwie równe części i obciążonej równomiernie na całej długości zgodnie ze schematem na Rys.3. Dodatkowo, w lewym węźle przyjęto wymuszenie kinematyczne po kierunku osi belki o wartości 1cm. Połączenie teleskopowe zostanie zdefiniowane w środku rozpiętości. Między łączone elementy wstawiono krótki ( ) element (teleskop) o sztywności giętnej równej sztywności łączonych elementów, natomiast sztywność podłużna została zredukowana do wartości bliskiej zeru poprzez przyjęcie małego pola przekroju (0.0001cm2). Pożądane sztywności osiągnięto z użyciem profilu o przekroju „Ogólnym” (możliwość definiowania właściwości geometrycznych samodzielnie). Ocena poprawności modelu została wykonana na podstawie analizy przebiegu sił przekrojowych oraz deformacji belki.
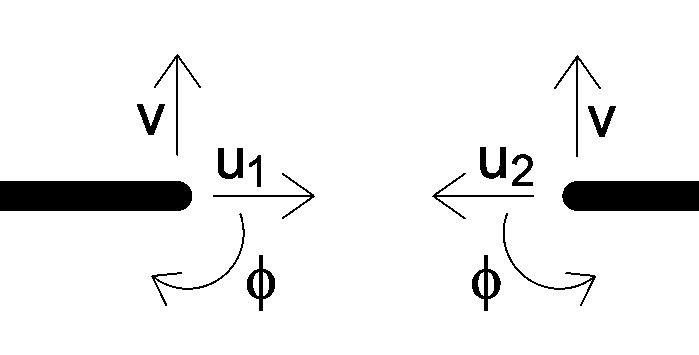 Rys.1. Idea połączenia teleskopowego. u i v są równe dla końców łączonych elementów. Rys.1. Idea połączenia teleskopowego. u i v są równe dla końców łączonych elementów. |
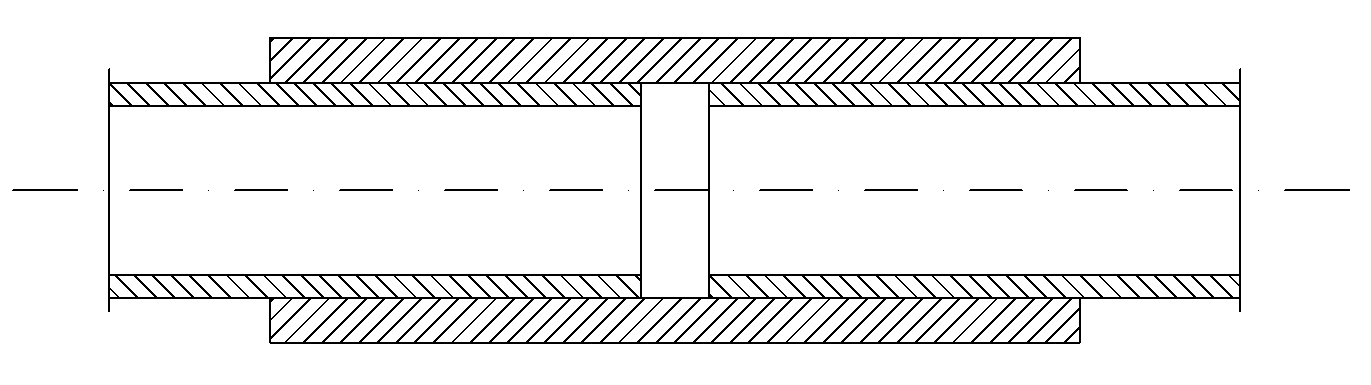 Rys.2. Przykład połączenia teleskopowego. Połączenie dwóch rur poprzez nasunięcie rury o większej średnicy Rys.2. Przykład połączenia teleskopowego. Połączenie dwóch rur poprzez nasunięcie rury o większej średnicy |
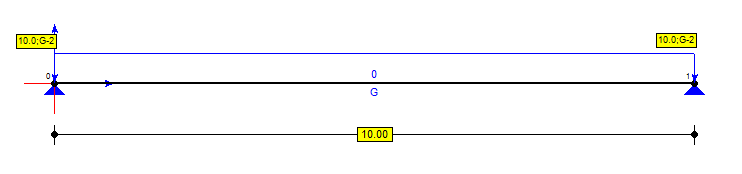
Rys.3. Schemat analizowanej belki wolnopodpartej
Procedura (Soldis PROJEKTANT v8.5)
Sposób definiowania geometrii, podpór oraz obciążenia można znaleźć w Procedurach.
Wyodrębnienie łącznika
- [a] Kliknij na element LPM, a następnie z paska narzędzi wybierz Podziel pręt.

- [b] W oknie dialogowym Podziel pręt wybierz Poprzez punkt podziału i podaj Długość równą 5 metrów (środek belki). Zatwierdzając dane przyciskiem OK belka zostanie podzielona na połowę.
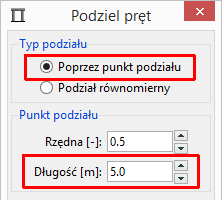 Aby wyodrębnić łącznik powtórz czynności [a-b] dla przęsła lewego wpisując Długość równą 4.95.
Aby wyodrębnić łącznik powtórz czynności [a-b] dla przęsła lewego wpisując Długość równą 4.95.
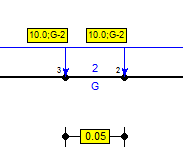
Definicja profilu łącznika
Przykłady definicji profili dla różnych typów elementów dostępne są tutaj.
- Otwórz Edytor profili i skopiuj profil belki.
- Zmień sztywność podłużną profilu.
- Kliknij dwukrotnie LPM i w panelu Przekrój wybierz Specjalne > Ogólny.
- W panelu Edycja przekroju wpisz wartość Jx równą 11770 cm4 oraz pole przekroju A równe 0.0001 cm4.
- Zaakceptuj zmiany przyciskiem OK.
Pozostałe charakterystyki przekroju, w analizowanym przypadku, nie mają znaczenia i można pozostawić wartości domyślne.
- Przypisz nowy profil do elementu łącznika zgodnie z instrukcjami w dokumentach dostępnych tutaj.
Wyniki
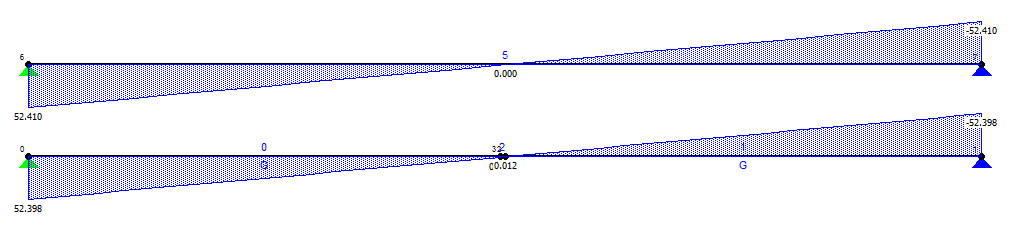
Przemieszczenie pionowe w środku rozpiętości wynosiło w obydwóch przypadkach 5.52cm. Przemieszczenie wzdłuż osi belki w przypadku schematu z łącznikiem wynosiło 1cm z jego lewej strony i 0cm z prawej. Poniżej przedstawiono wykresy sił przekrojowych przed i po wprowadzeniu łącznika teleskopowego.
Rys.4. Porównanie wykresów sił normalnych (model z łącznikiem u dołu).
 Rys.5. Porównanie wykresów sił tnących (model z łącznikiem u dołu).
Rys.5. Porównanie wykresów sił tnących (model z łącznikiem u dołu).
Rys.6. Porównanie wykresów momentów zginających (model z łącznikiem u dołu).
Dyskusja i podsumowanie
Różnica przemieszczeń wzdłuż osi z lewej i prawej strony łącznika teleskopowego udowadnia niezależność ruchu łączonych węzłów w tym kierunku, a siła normalna w elementach bliska zeru brak sztywności w kierunku osiowym. Dodatkowo, zgodne przemieszczenie pionowe w środku rozpiętości oraz brak różnic w przebiegu momentów zginających i sił tnących dowodzi, że wprowadzone połączenie w pełni wiąże obrót oraz przemieszczenie prostopadłe do osi łączonych elementów. Połączenie spełnia zatem postawione na wstępie wymagania.


