Stropodach
Stropodach składa się z płyt kanałowych o rozpiętości 6,00 m. Ciężar własny płyty to 2,6 kN/m2
Płyty stropowa
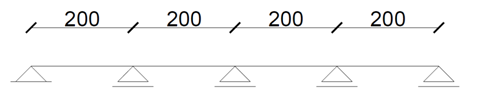
Rozstaw żeber przyjęto zgodnie ze schematem poniżej:
Wysokość płyty oszacowano z warunku smukłości płyty
\(h_f=(\frac{1}{30}\div\frac{1}{20})l=(\frac{1}{30}\div\frac{1}{20})\cdot 2,00=(0,066\div 0,10)m\)Przyjęto wstępnie \(h_f=10cm\)
Wysokość użyteczna płyty
\(a_1=C_{nom}+\phi_{st}+\frac{1}{2}\phi=35mm+8mm+8mm=51mm\) \(d=h_f-a_1=100mm-51mm=49mm\)Określenie minimalnego pola przekroju zbrojenia głównego
\(A_{s,min}=max\left\{\begin{array}{11} 0,26\cdot\frac{f_{ctm}}{f_yk}\cdot b_t\cdot d\\0,0013\cdot b_t\cdot d\end{array}\right.\) \(A_{s,min}=max\left\{\begin{array}{11} 0,26\cdot \frac{2,9}{500}\cdot 100\cdot 4,9\\0,0013\cdot 100\cdot 4,9\end{array}\right.=max\left\{\begin{array}{11} 0,74cm^2\\0,611cm^2\end{array}\right.=0,74cm^2\)Określenie maksymalnego przekroju pola zbrojenia głównego
\(A_{s,max}=0,04\cdot A_c=0,04\cdot 100\cdot 10=40 cm^2\)Maksymalny rozstaw prętów zbrojenia głównego
\(s_{max,slabs}=min\left\{\begin{array}{11}2\cdot h\\250\end{array}\right.=min\left\{\begin{array}{11}2\cdot 100\\250\end{array}\right.=min\left\{\begin{array}{11}200\\250\end{array}\right.=200mm\)Zebranie obciążeń działających na strop.
| Lp. | Rodzaj obciążenia | Obciążenie charakterystyczne [kN/m2] | Współczynnik obciążenia ɣf | Obciążenie obliczeniowe [kN/m2] |
|
Obciążenie stałe |
||||
| 1. |
Zewnętrzne obciążenie |
1,368 |
1,35 |
1,849 |
| 2. |
Płyta monolityczna 10 cm |
2,5 |
1,35 |
3,375 |
|
Razem obciążenia stałe : |
3,87 |
1,35 |
5,22 |
|
|
Obciążenie zmienne |
||||
|
Obciążenie charakterystyczne użytkowe |
9,0 |
1,5 |
13,5 |
|
|
Razem obciążenia zmienne |
9,0 |
1,5 |
13,5 |
|
|
Razem |
12,87 |
– |
18,72 |
|
Wartość obliczeniowa obciążeń to \(18,72 kN/m^2\)
Obciążenie przypadające na jedno żebro należy obliczyć z ich rozstawu czyli 2,00 m.
Zwiększenie obciążenia o 10% wynika z próby oszacowania ciężaru własnego żebra.
\(18,72\cdot 2\cdot 1,1=41,18[kN/m]\)Przyjęto schemat belki ciągłej, wieloprzęsłowej czyli wartość momentu maksymalnego należy przemnożyć razy 0,8.
\(M_{Ed}=\frac{41,18\cdot 6^2}{8}\cdot 0,8 = 148,25[kNm]\)Obliczenie wysokości użytecznej
Wysokość użyteczna obliczono dla przyjętego stopnia zbrojenia ρ=1,1%
\( \xi=\rho\cdot \frac{f_{yd}}{\eta\cdot f_{cd}}=0,011\cdot \frac{435}{1,0\cdot 21}=0,228\) \( A_0=\xi\cdot (1-0,5\cdot \xi)=0,228\cdot (1-0,5\cdot 0,228)=0,202\) \( d_{req}=\sqrt{\frac{M_{Ed}}{\eta\cdot f_{cd}\cdot b_w\cdot A_0}}=\sqrt{\frac{263,55}{1\cdot 21\cdot 0,35\cdot 0,202}}=0,202\)\(h=0,374\)
Przyjęto żebro o wymiarach 0,35×0,7 m
|
Lp. |
Rodzaj obciążenia |
Obciążenie charakterystyczne [kN/m] |
Współczynnik obciążenia ɣf |
Obciążenie obliczeniowe [kN/m] |
| Obciążenie stałe | ||||
|
1. |
Zew.obc.stałe 3,87 [kN/m2]*2 m=7,74 kN/m |
7,74 |
1,35 |
10,44 |
|
2. |
Ciężar własny żebra 25 [kN/m3]*0,25 m*0,7 m=2,5 kN/m |
4,375 |
1,35 |
5,91 |
|
Razem obciążenia stałe : |
12,12 |
1,35 |
14,63 |
|
|
Obciążenie zmienne |
||||
|
Obciążenie charakterystyczne użytkowe: 9,0 [kN/m2]*2 m |
19,0 |
1,5 |
28,5 |
|
|
Razem obciążenia zmienne: |
19,0 |
1,5 |
28,5 |
|
|
Razem: |
29,87 |
– |
43,13 |
|