Opis problemu
W przypadku dźwigarów wykonanych rur prostokątnych, w każdym profilu istnieją trzy istotne parametry, które mogą podlegać modyfikacji (szerokość, wysokość oraz grubość ścianki). Ze względu na liczne i złożone warunki projektowe SGN oraz SGU, aby otrzymać konstrukcję optymalną, konieczne jest operowanie wszystkimi parametrami jednocześnie. W dokumencie przedstawiono procedurę automatycznego doboru parametrów profili pasów i skratowania minimalizującego masę na przykładzie dźwigara stalowego [1565] w konstrukcji zadaszenia wspornikowego [1557] (redukcja o 26%).
Metody
Kształtowanie profili pasów oraz skratowania wykonano przy użyciu procedury optymalizacji w programie Soldis PROJEKTANT. Celem optymalizacji było znalezienie parametrów rur prostokątnych dla których masa dźwigara jest najmniejsza. Przyjęto 9 zmiennych projektowych – po trzy na każdy profil (szerokość, wysokość oraz grubość ścianki). Zakres oraz skok dla poszczególnych parametrów przedstawiono w Tab.1. W trakcie optymalizacji uwzględniono wszystkie niezbędne warunki nośności oraz użytkowalności zgodnie z 1655.
Ze względu na elementy stochastyczne dostępnych algorytmów wymiarowania optymalizację przeprowadzono kilkukrotnie zapamiętując tylko wyniki poprawiające poprzednio osiągniętą wartość masy konstrukcji.
Uwaga! Przedstawiony problem można również rozwiązać poprzez dobór profili z katalogu (przykład w 1417).
Tab.1: Zmienne projektowe dla analizowanych profili.
| Parametr | Min [mm] | Max [mm] | Skok [mm] |
|---|---|---|---|
| Szerokość – S | 30 | 150 | 2 |
| Wysokość – H | 30 | 150 | 2 |
| Grubość – t/g | 1 | 10 | 1 |
Procedura
Poniższa procedura bazuje na modelu z dokumentu 1655 (załączony również do niniejszego dokumentu).
Definicja zmiennych projektowych – grubość ścianek
Uwaga! W przypadku rury prostokątnej grubości ścianek pionowych (t) oraz poziomych (g) w Solds PROJEKTANT traktowane są niezależnie. Aby powiązać ich wartości, w przedstawionym zadaniu, użyto Parametr użytkownika (opis poniżej). W sytuacji gdy dopuszczalne są różne grubości ścianek (np. przekrój skrzynkowy spawany) parametry t i g należy zdefiniować wprost w Przekroju użytkownika (kolejna sekcja).
- Przejdź do Analiza > Optymalizacja > Menadżer zmiennych.
- W oknie Zmienne projektowe wybierz Dodaj zmienną projektową.
- Z listy wybierz typ Parametr użytkownika.
- [a] Zaznacz nowy wiersz na liście Zmienne projektowe.
- [b] Z paska narzędzi u dołu wybierz Edytuj zmienną projektową i podaj nazwę Pas górny – ścianka.
- [c] W panelu Definicja parametru podaj danej jak poniżej.
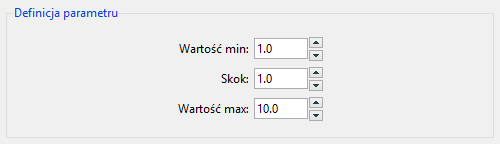
- [d] Skopiuj zmienną projektową. Na liście Zmienne projektowe zaznacz zmienną Pas górny – ścianka i z paska narzędzi u dołu wybierz Skopiuj zmienną projektową.
- [e] Powtórz czynności [a-c] zmieniając nazwę na Pas dolny – ścianka.
- Powtórz czynności [d-e] zmieniając nazwę na Skratowanie – ścianka.
Definicja zmiennych projektowych – profile
- [f] W oknie Zmienne projektowe wybierz Dodaj zmienną projektową.
- [g] Z listy wybierz typ Przekrój użytkownika.
- [h] Zmień nazwę na Pas górny (patrz [a-b]).
- [i] Z listy rozwijanej wybierz Profil o numerze 3 (pas górny).
- [j] W panelu Parametry przekroju wybierz Rodzaj: Definiowane oraz Nazwa: Rura prostokątna.
- [k] W panelu Wymiary zaznacz zmienne H, S, g, t oraz ustaw ich parametry zgodnie z rysunkiem poniżej. Numer Parametru dla g i t należy podać zgodnie z numerem parametru użytkownika na liście z lewej strony.
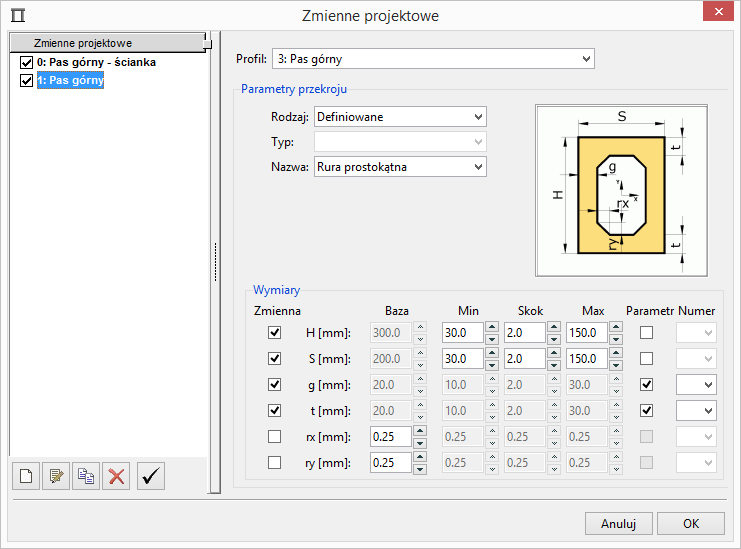
- Powtórz czynności [f-k] dla pasa dolnego oraz skratowania zmieniając nazwy, przypisanie profilu (patrz [i]) oraz numer parametru użytkownika dla zmiennych g i h (patrz [k]).
Definicja i uruchomienie optymalizacji
- Przed rozpoczęciem optymalizacji zapisz projekt.
- Przejdź do Analiza > Optymalizacja > Monitor procesu optymalizacji.
- W oknie Monitor pozostaw domyślne ustawienia. Zwróć uwagę na Wytężenie graniczne równie 0.8 (zgodnie z założeniami zadania 80%) oraz Siłę ograniczeń równą 1.5 (komentarz poniżej).
- Siła ograniczeń określa poziom „rozmiękczenia” ograniczeń (wartość od 0 do 3). Umożliwienie algorytmowi nieznacznego przekroczenia limitu ugięcia sprzyja lepszemu przeszukaniu rozwiązań. Aby zmusić algorytm optymalizacji do bezwzględnego przestrzegania ograniczeń zmień wartość Siła ograniczeń na 3.
- Aby rozpocząć optymalizację wybierz Uruchom.
- Po zakończeniu optymalizacji program umożliwia przebudowę do najlepszego wyniki. Wybierz Tak jeżeli osiągnięty wynik jest satysfakcjonujący.
Optymalizację należy powtórzyć kilkukrotnie zapamiętując wyniki, które redukują masę poniżej poziomu ostatnio osiągniętego. Zalecaną metodą jest zapisanie projektu każdorazowo po przebudowie modelu i zaakceptowaniu zmian (warunki nośności, konstrukcyjne, tolerancja w spełnieniu ograniczeń itd.).
Wyniki
W Tab.2. oraz Rys.1-2 przedstawiono szczegóły oraz ilustrację rozwiązania wyjściowego oraz otrzymanych w wyniku użycia opisanej procedury. W ostatniej kolumnie Tab.2 dodano wyniki dla rozwiązania „Optymalny 2” z zaokrąglonymi wymiarami profili.
Tab.2: Parametry wiązara wyjściowego oraz dwóch osiągniętych rozwiązań (w nawiasach przedstawiono maksymalne wytężenie elementów).
| Cecha/Profil | Wyjściowy | Optymalny 1 | Optymalny 2 | Optymalny 2′ |
|---|---|---|---|---|
| Masa | 52.8kg | 43.7kg | 39.3kg | 39.5kg |
| Pas górny | 50x50x3 (55%) | 32x34x3 (70%) | RP32x38x3 (68%) | RP30x40x3 (68%) |
| Pas dolny | 40x60x4 (72%) | 90x46x3 (72%) | RP52x48x4 (80%) | RP50x50x4 (88%) |
| Skratowanie | 40x40x3 (47%) | 30x30x3 (67%) | RP34x30x2 (89%) | RP35x30x2 (89%) |
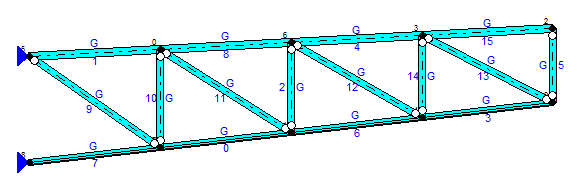
Rys.1: Wiązar wyjściowy.
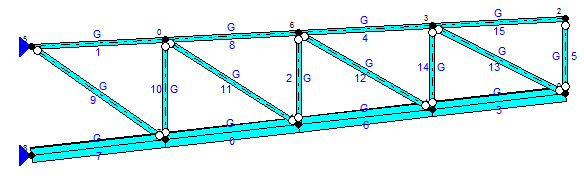
Rys.2: Rozwiązanie optymalne 1.
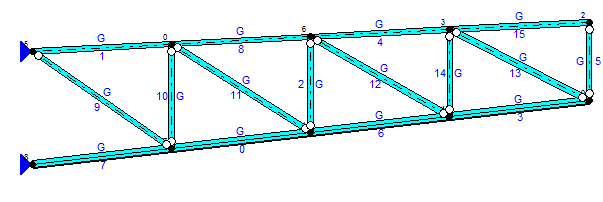
Rys.3: Rozwiązanie optymalne 2.
Podsumowanie
Procedura optymalizacji umożliwiła znalezienie dwóch rozwiązań spełniających warunki SGN oraz SGU, gdzie maksymalna redukcja masy wyniosła 26% i nie uległa istotnej zmianie po zaokrągleniu otrzymanych wymiarów (Tab.2. – ostania kolumna). Rozwiązania optymalne charakteryzuje bardziej równomierne wytężenie poszczególnych elementów, a zatem lepsze wykorzystanie materiału. Otrzymane wyniki potwierdzają skuteczność przedstawionej metody jako narzędzia do automatycznego określenia wymiarów profili minimalizującego masę konstrukcji przy zachowaniu wszystkich warunków projektowych. Warto zwrócić uwagę na fakt, że procedurę w przedstawionej formie można użyć również w sytuacji, gdy podstawowym celem jest znalezienie profili spełniających warunki projektowe, a nie minimalizacja masy.
