Cel
Redukcja ugięcia wiązara kratowego [55] z użyciem algorytmu optymalizacji.
Opis problemu
W przypadku belek modelowanych zgodnie z teorią Bernoulliego-Euler (stosowana standardowo w analizach prętowych konstrukcji budowalnych) przemieszczenie prostopadłe do osi wynika tylko i wyłącznie ze zginania (powstanie krzywizny). W przypadku wiązara kratowego, ugięcie stanowi sumaryczny efekt ugięcia wynikającego ze „zginania” (rozciąganie pasów) oraz deformacji poprzecznych wywołanych „ścinaniem” (rozciąganie/ściskanie skratowania). Wpływ deformacji poprzecznych na całkowite ugięcie wiązara zależy od wielu czynników (stosunek sztywności skratowania do pasów, rozkład sił w skratowaniu, proporcji wysokości do długości wiązara, itd) i jest trudny do oszacowania. Redukcja ugięcia tylko poprzez zwiększenie pasów może być zatem nieefektywna.
Metody
Redukcję ugięcia wiązara wykonano przy pomocy procedury optymalizacji w programie Soldis PROJEKTANT. Celem optymalizacji było dobranie profili minimalizujących masę wiązara przy uwzględnieniu limitu ugięć 20mm (w projekcie wyjściowym ugięcie wynosi 26mm). Jak zmienne projektowe przyjęto profile skratowania oraz pasów. Dyskretne wartości zmiennych dobierane były ze wskazanego zbioru dopuszczalnych profili (niezależnego dla każdej zmiennej). Przyjęto, że pasy mają być wykonane z IPE, a skratowanie z rur kwadratowych o wymiarach 40-90mm (dowolna grubość ścianki). W trakcie optymalizacji uwzględniono wszystkie niezbędne warunki nośności oraz użytkowalności. W celu wymuszenia żądanego limitu ugięcia dodano regułę wymiarowania „Dopuszczalne przemieszczenia”. Przy definicji optymalizacji przyjęto akceptowalny próg wytężenia konstrukcji na poziomie 80%. Uwzględniając powyższe założenie, ograniczenie dla przemieszczenia należy ustalić na poziomie 25mm. Algorytm optymalizacji dążąc do spełnienia warunku o maksymalnym 80% wytężeniu dla wszystkich reguł wymiarowania, ograniczy ugięcia do oczekiwanych 20mm.
Ze względu na elementy stochastyczne dostępnych algorytmów wymiarowania optymalizację przeprowadzono kilkukrotnie zapamiętując tylko wyniki poprawiające poprzednio osiągniętą wartość masy konstrukcji.
Procedura (Soldis PROJEKTANT v8.5)
Poniższa procedura bazuje na modelu z dokumentu 987.
Dodanie ograniczenia dla przemieszczeń
- Przejdź do Analiza > Wymiarowanie > Przypisz regułę wymiarowania.
- W listy wybierz komponent Przemieszczenia dopuszczalne.
- Kliknij LPM na element pasa dolnego znajdujący się w środku rozpiętości i zatwierdź ŚPM lub przyciskiem Zastosuj.
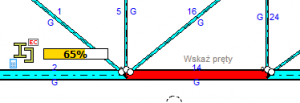
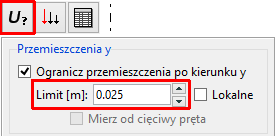
- Wejdź w Ustawienia ograniczeń i w panelu Przemieszczenia y ustal limit 0.025m pozostawiając resztę warunków nieaktywną.
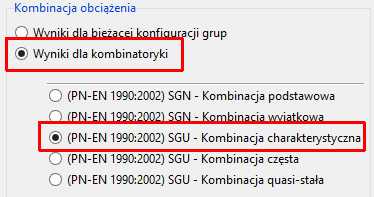
- Następnie wejdź w Kombinacja obciążenia i wybierz Wyniki dla kombinatoryki oraz SGU – Kombinacja charakterystyczna.
- Zatwierdź ustawienia przyciskiem Ok.
Definicja zmiennych projektowych
- Przejdź do Analiza > Optymalizacja > Menadżer zmiennych.
- W oknie Zmienne projektowe wybierz Dodaj zmienną projektową.
- Z listy wybierz typ Przekrój standardowy.
- [a] Zaznacz nowy wiersz na liście Zmienne projektowe, z paska narzędzi u dołu wybierz Edytuj zmienną projektową i podaj nazwę Pas górny.
- [b] Z listy rozwijanej wybierz Profil o numerze 1 (pas górny).
- [c] W panelu Katalog przekrojów wybierz Walcowane, Dwuteownik oraz zaznacz na liście wszystkie przekroje typu IPE i kliknij przycisk > (przy zaznaczaniu używaj kombinacji klawiszu Shift/Ctrl oraz LPM).
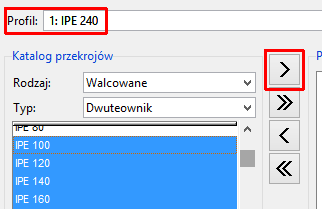
- [d] Skopiuj zmienną projektową. Na liście Zmienne projektowe zaznacz zmienną Pas górny i z paska narzędzi u dołu wybierz Skopiuj zmienną projektową.
- Dla skopiowanej zmiennej powtórz czynności [a-c] ustawiając odpowiedni Profil dla pasa dolnego oraz nazwę Pas dolny.
- W podobny sposób utwórz dwie pozostałe zmienne dla krzyżulców oraz słupków definiując Przekroje do sprawdzenia jako rury kwadratowe od 40 do 90mm (wszystkie grubości ścianki).
Definicja i uruchomienie optymalizacji
- Przed rozpoczęciem optymalizacji zapisz projekt.
- Przejdź do Analiza > Optymalizacja > Monitor procesu optymalizacji.
- W oknie Monitor pozostaw domyślne ustawienia. Zwróć uwagę na Wytężenie graniczne równie 0.8 (zgodnie z założeniami zadania 80%) oraz Siłę ograniczeń równą 1.5 (komentarz poniżej).
- Siła ograniczeń określa poziom „rozmiękczenia” ograniczeń (wartość od 0 do 3). Umożliwienie algorytmowi nieznacznego przekroczenia limitu ugięcia sprzyja lepszemu przeszukaniu rozwiązań. Aby zmusić algorytm optymalizacji do bezwzględnego przestrzegania ograniczeń zmień wartość Siła ograniczeń na 3.
- Aby rozpocząć optymalizację wybierz Uruchom.
- Po zakończeniu optymalizacji program umożliwia przebudowę do najlepszego wyniki. Wybierz Tak jeżeli osiągnięty wynik jest satysfakcjonujący.
Optymalizację należy powtórzyć kilkukrotnie zapamiętując wyniki, które redukują masę poniżej poziomu ostatnio osiągniętego. Zalecaną metodą jest zapisanie projektu każdorazowo po przebudowie modelu i zaakceptowaniu zmian (warunki nośności, konstrukcyjne, tolerancja w spełnieniu ograniczeń itd.).
Wyniki
Tab.1: Parametry wiązara wyjściowego oraz dwóch osiągniętych rozwiązań. W nawiasach przedstawiono wytężenie elementu.
| Cecha/Projekt | Wyjściowy | Optymalny 1 | Optymalny 2 |
|---|---|---|---|
| Masa/Ugięcie | 1653kg/26mm | 2551kg/17.5mm | 2074kg/21.8mm |
| Pas górny | IPE240 (89%) | IPE330 (45%) | IPE300 (54%) |
| Pas dolny | IPE220 (65%) | IPE300 (39%) | IPE240 (44%) |
| Słupki | RK60x60x4 (81%) | RK50x50x6.3 (72%) | RK60x60x4 (59%) |
| Krzyżulce | RK60x60x4 (64%) | RK60x60x5 (78%) | RK70x70x3 (67%) |

Rys.1: Wiązar wyjściowy.

Rys.2: Rozwiązanie optymalne 1.

Rys.3: Rozwiązanie optymalne 2.
Podsumowanie
Procedura optymalizacji umożliwiła znalezienie dwóch rozwiązań o różnej wartości masy oraz maksymalnego ugięcia. W obydwu przypadkach znacznemu zwiększeniu uległy pasy, co dowodzi że deformacje poprzeczne (w wyniki rozciągania skratowania) w tym przypadku nie są znaczące. Dalsza decyzja o wyborze konkretnego rozwiązania zależy od możliwości przekroczenia wskazanego limitu ugięcia. Rozwiązanie pierwsze redukuje ugięcie do 17.5mm, ale jednocześnie zwiększa masę do ponad 2500kg. W rozwiązaniu drugim masa wzrasta do 2000kg, ale ugięcie wynosi 21.8mm.
