Opis problemu
Przy relatywnie wysokich żelbetowych halach jednokondygnacyjnych wpływ efektów nieliniowych może być znaczącym czynnikiem wpływającym na nośność słupów. Bazując na wynikach statyki liniowej, określenie wpływu smukłości (dodatkowego mimośrodu działania siły) jest wprost zależne od siły krytycznej elementu, a w konsekwencji od przyjętego współczynniki długości wyboczeniowej. Przyjmując klasyczny schemat słupa wspornikowego otrzymujemy μ=2.0. Norma PN-B-03264 [2], w przypadku dachu o konstrukcji sztywnej, proponuje wartość niższa μ=1.6, podczas gdy norma PN-84/B-03264 [3] umożliwia dalszą redukcję w zależności od liczby współpracujących słupów, aż do poziomu μ=1.2 (sześć słupów). Brak jest natomiast wyodrębnienia analizowanego przypadku w normie PN-EN 1992 [1]. Powstaje zatem pytanie, skąd taka rozbieżność w normach polskich i czy brak wyraźniej informacji o możliwości redukcji w PN-EN 1992 [1] nie jest przypadkiem negacją „zbyt optymistycznej” wartości zaproponowanej przez normy polskie. Niniejszy dokument przedstawia wpływ współpracy słupów na długość wyboczeniową w zależności od ich liczby oraz schematu obciążenia i umożliwia sformułowanie wniosków częściowo odpowiadających na postawione pytania.
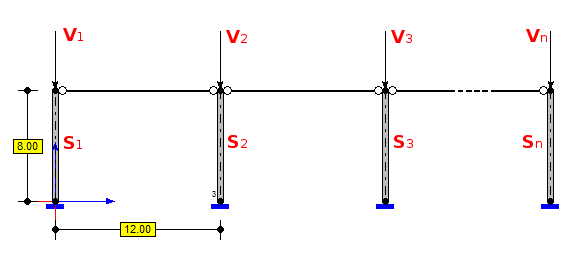
Rys.1. Model analizowanego modelu
Metody
Analizie poddano różne konfiguracje szeregu słupów (30×45, B35/45, pominięto efekty zarysowania, reologiczne oraz wpływ zbrojenia) połączonych przegubowo sztywnymi ryglami (materiał ogólny: EA=9.(9)e12N) i obciążonych siłami Vn (Rys.1). W programie Soldis PROJEKTANT v8.5 przygotowano 11 modeli obliczeniowych różniących się liczbą słupów oraz schematem obciążenia (Tab.1, modele załączono do niniejszego dokumentu). Dla każdego przypadku wykonano analizę stateczności (panel główny > Analiza > Stateczność) uzyskując mnożnik siły krytycznej równy w analizowanym przykładzie, co do wartości, sile krytycznej wyrażonej w kN (siła normalna w słupach tracących stateczność, od przyjętego obciążenia wynosi 1kN). Współczynnik długości wyboczeniowej słupów określono zgodnie z procedurą opisaną tutaj.
Uwaga! Prezentowana analiza dotyczy tylko wyboczenia w płaszczyźnie układu.
Wyniki
Otrzymane wyniki przedstawiono w Tab.1. W bloku „Schemat/obciążenie” poszczególne kolumny zawierają informacje o wartości siły przyłożonej do słupa. Symbol „-” oznacza brak słupa. Przykładowa postać wyboczenia została zaprezentowana na Rys.2.
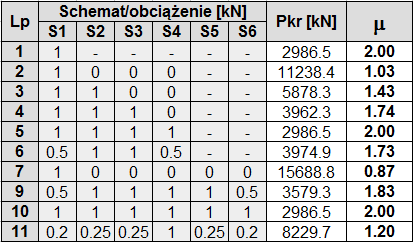
Tab.13. Wartości sił krytycznych oraz współczynnik długości wyboczeniowej. „Schemat/obciążenie” – opis w tekście.
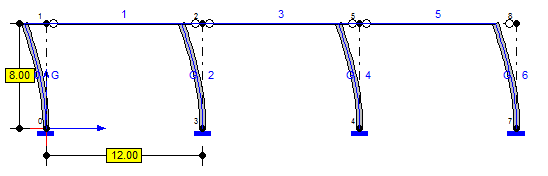
Rys.2. Przykładowa postać wyboczenia dla układu trzech słupów równo obciażonych.
Dyskusja
Współczynnik długości wyboczeniowej uzyskany dla modelu nr 1 (pojedynczy słup wspornikowy) potwierdza poprawność użytej procedury (patrz Tab.1). Dodając kolejne trzy nieobciążone słupy (model 2) μ spada do 1.03. Efekt stabilizacji przesuwu górnego węzła jest proporcjonalny do liczby dodatkowych słupów. Dla sześciu słupów, z których tylko jeden jest obciążony (model 7), wartość μ wynosi już tylko 0.87. W miarę dodawania kolejnych nieobciążonych słupów redukcja zmierza asymptotycznie do wartości 0.7 (całkowite zablokowanie przesuwu węzła górnego). Obciążenie większej liczby słupów, powoduje spadek siły krytycznej (patrz kolejno modele 2, 3, 4, 5), aż do wartości uzyskanej dla modelu 1 (pojedynczy słup wspornikowy). Spadek μ do poziomu 1.0 przy obciążeniu wszystkich słupów nie zależy od ich liczby (porównaj model 5 i 10). W przypadku prawdopodobnej redukcji obciążenia na słupach skrajnych do połowy (model 6 oraz 9) μ ulega redukcji do 1.74 oraz 1.83 odpowiednio dla układu czterech i sześciu słupów. Warto zauważyć, że w tak przyjętym schemacie obciążenia, im mniejsza jest liczba słupów tym większa wartość siły krytycznej co jest wynikiem proporcji liczby słupów wybaczających się do stabilizujących. W modelu 11-tym przedstawiono przykładowy rozkład obciążenia dla 6-cio słupowego układu, przy którym μ zostaje zredukowane do 1.2.
W prezentowanych analizach sztywność elementów nie została zredukowana ze względu na zarysowanie, zjawiska reologiczne oraz rozkład zbrojenia. Jeżeli jednak uwzględnienie rzeczywistej sztywności elementu żelbetowego będzie dokonywane poprzez korektę sztywności giętnej na całej jego długości, a nie tylko w obszarach silnie zginanych, sformułowane wnioski nie ulegną zmianie – istotna jest wzajemna sztywność giętna słupów.
Podsumowanie
Stosując wartość wspł. długości wyboczeniowej poniżej 2.0 zakładamy (mniej lub bardziej świadomie), że analizowany szereg słupów jest nierównomiernie obciążony lub, co nie było przedmiotem niniejszego opracowania, analizowany słup jest mniej sztywny od sąsiednich/sąsiedniego (np. zastosowano bastion). Wartość μ=1.6 proponowana w PN-B-03264 [2], bazując na otrzymanych wynikach, zakłada zróżnicowanie sił osiowych w słupach większe niż tylko ich dwukrotna redukcja w słupach skrajnych. Natomiast redukcja μ do poziomu 1.2 proponowanego w PN-84/B-03264 [3] występuje tylko przy nieznacznym obciążeniu słupów stabilizujących (ok 25% siły krytycznej). Równomierne obciążenie wszystkich słupów w realnych sytuacjach jest mało prawdopodobne jednak, ponieważ trudno o uniwersalną statystykę jak kształtuje się miarodajny schemat obciążenia przy wyboczeniu, każda konstrukcja powinna być rozpatrywana indywidualnie. Brak zatem ogólnego zapisu w PN-EN 1992 o możliwej redukcji μ dla współpracujących słupów wydaje się uzasadniony. Jeżeli wartość μ=2.0 nie jest do zaakceptowania, należy przeprowadzić analizę stateczności zgodnie z przedstawioną procedurą uzupełniając model, o ile to wymagane, o osłabienie sztywności słupów w wyniku zarysowania, efektów reologicznych oraz uwzględnienie rozkładu zbrojenia.
Bibliografia
- PN-EN 1992-1-1 „Projektowanie konstrukcji z betonu: Reguły ogólne i reguły dla budynków”
- PN-B-03264 „Konstrukcje betonowe, żelbetowe, sprężone: Obliczenia statyczne i projektowanie”
- PN-84/B-03264 „Konstrukcje betonowe, żelbetowe i sprężone. Obliczenia statyczne i projektowanie”
