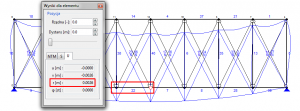
Opis problemu
Określenie sił wewnętrznych i przemieszczeń w układzie stężającym.
Metody
Analiza statyczna stężenia jest procesem iteracyjnym. Pod wpływem przyłożonego obciążenia imperfekcyjnego qd, następuje ugięcie tężnika o wartość δq. Z uwagi na zwiększoną strzałkę ugięcia, należy skorygować wartość równoważnego obciążenia ciągłego, zgodnie ze Wz.1.
Wz.1: Równoważne obciążenie ciągłe (destabilizujące)
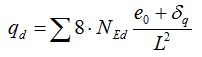
Odczytuje się ugięcie i ponownie koryguje obciążenie. Iteracje powtarza się do uzyskania odpowiedniej zbieżności kolejnych wartości ugięć. Ze względu na cięgnowy charakter pracy skratowania (przenoszenie tylko sił rozciągających) należy posłużyć się analizą nielinową.
Procedura (Soldis PROJEKTANT v8.5)
Procedurę zaprezentowano dla pierwszego przypadku obciążenia stężenia – tylko siłami imperfekcyjnymi (należy wyłączyć wszystkie grupy obciążeń oprócz Imperfekcje (1)). Procedura obowiązuje także dla pozostałych przypadków.
Pierwsza iteracja
- Z paska głównego wybierz zakładkę Analiza.
- Kliknij w strzałkę pod kafelkiem Statyka i wybierz Statyka nieliniowa.
W przypadku wyboru opcji Statyka liniowa, pojawi się komunikat informujący „Do prawidłowej pracy cięgien wymagana jest analiza nieliniowa. Kontynuować analizę liniową?”. Wybierz Nie, a następnie postępuj zgodnie z punktami powyżej.
- Z panelu Przeglądanie wyników dla statyki wybierz Wykres przemieszczeń układu.
- Kliknij dwukrotnie LPM w środkowy pręt pasa dolnego.
- Przesuń suwak w stronę osi symetrii konstrukcji, w celu odczytania maksymalnego przemieszczenia.
Wyjaśnienie oznaczeń: u – przemieszczenie wzdłuż osi, v – przemieszczenie prostopadłe do osi, r – przemieszczenie wypadkowe, fi – kąt obrotu przekroju.
Dalsze iteracje
- Wróć do zakładki Modelowanie w pasku głównym.
- Zaznacz obciążenia ciągłe, klikając w nie LPM, a następnie kliknij PPM i wybierz Edytuj.
- W oknie Obciążenie w opcji Wartość [kN/m] w wierszach A i B wpisz .
- Powtórz czynności z punktu Pierwsza iteracja.
Procedurę powtórz do uzyskania zbieżności kolejnych wyników.
Tab.1: Wyniki iteracji – przypadek (1) do (5).
| Iteracja 1 | Iteracja 2 | Iteracja 3 | Iteracja 4 | |||||
|---|---|---|---|---|---|---|---|---|
| Przypadek | qd [kN/m] | δq [mm] | qd [kN/m] | δq [mm] | qd [kN/m] | δq [mm] | qd [kN/m] | δq [mm] |
| (1) | 0.745 | 26 | 0.797 | 28 | 0.801 | 28 | – | – |
| (2) | 0.144 | 54 | 0.165 | 55 | 0.165 | 55 | – | – |
| (3) | 0.512 | 62 | 0.596 | 65 | 0.600 | 66 | 0.602 | 66 |
| (4) | 0.198 | 142 | 0.273 | 144 | 0.274 | 144 | – | – |
| (5) | 0.551 | 99 | 0.696 | 104 | 0.703 | 104 | – | – |
Siły wewnętrzne
- Po wykonaniu iteracji z panelu Przeglądanie wyników dla statyki wybierz Normalne.
Tab.2: Ekstremalne siły normalne w elementach stężenia – przypadek (1) do (5).
| Przypadek | Płatew | Wiązar | Stężenie |
|---|---|---|---|
| (1) | -8.9 | -9.0 | 8.7 |
| (2) | -28.1 | -26.7 | 27.2 |
| (3) | -23.0 | -22.3 | 22.4 |
| (4) | 7.5 | -10.8 | 54.3 |
| (5) | 5.3 | -7.9 | 38.9 |
Przypadek (2) okazuje się miarodajny do ponownego sprawdzenia płatwi i wiązara, ze względu na dodatkową siłę ściskającą. Przypadek (4) jest miarodajny do zwymiarowania prętów skratowania stężenia.
Załączniki do pobrania
| Plik | Opis | Wielkość pliku | Pobrania |
|---|---|---|---|
hala_stalowa_2d_stężenia
|
502 KB | 202 |